An ALU for MIPS

• Let's begin by looking at the green card to find the instructions that need the ALU.
  • The green card contains only a "core" instruction set.
    • Integer only, we are not worried about fp (yet)
    • But we may need to worry about the pseudo-instructions
    • A more complete set is in appendix A, section 10
  • Looking over the list I see the following math instructions
    • add, addi, addiu, addu
    • and, andi
    • nor
    • or
    • ori
    • sub, subu
  • For now, we can ignore the u instructions,
  • And there is no difference between add and addi for the ALU
  • So the list is add, sub, and, or, nor
  • But a closer look gives us a few more
    • slt and slti both need the ALU to do a comparison
      • slt dest, src1, src2
      • If the src1 is less than src2, the result is a 1, otherwise a 0
      • This can be done with a subtract and look at the resulting MSB
    • as does BEQ and BNE
      • This can be done by checking to see if the output of the ALU is 0.
  • So in addition to the previous list, we need a equal operator.
• The general approach is to build a series of 1 bit ALU units and hook them together as you do building a ripple-carry adder.
• In order to match the architecture of MIPS, we will follow their construction technique.
  • Looking at the diagram on page 265, we see the ALU has
    • Two word sized inputs (32 bits)
    • A word sized output
    • A 1 bit zero line (true if the output is zero)
    • A 4 bit ALU control line
  • The important part is to match the operations with the 4 bit control line
  • The control line is, for some strange reason (See page B-36)

  • ALU Control	Function
    0000	AND
    0001	OR
    0010	add
    0110	subtract
    0111	Set on Less Than
    1100	NOR
    0000	AND

  • The last two digits control a 4 input mux.
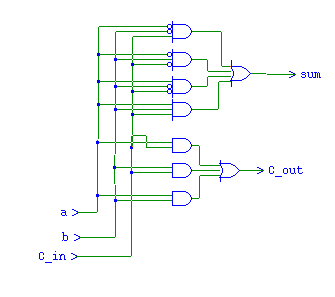
• Start by building a circuit that
  • Takes two one bit inputs, a and b
  • A two bit control line.
  • Outputs a·b if the line is 00
  • Outputs a + b if the line is 01
  • It looks something like this
  • 
  • By the way, you might want to change the default mux orientation
  • 
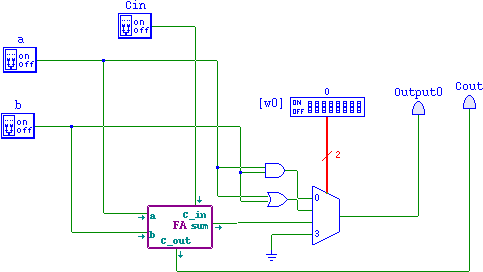
• Next build a full adder
  • You should have looked at this in 125.
  • You will look at this in homework 5.
  • And you should read about it on pages B-26 through B-29.
  • But you can just take on faith
    • Three inputs: a,b, CarryIn
    • Two outputs sum, CarryOut
    • sum = a·b·CarryIn +a·b·CarryIn +a·b·CarryIn +a·b·CarryIn
    • CarryOut = a · CarryIn + b · CarrayIn + a · b
    • 
  • Hook this full adder in to input 2 of the mux
    • 
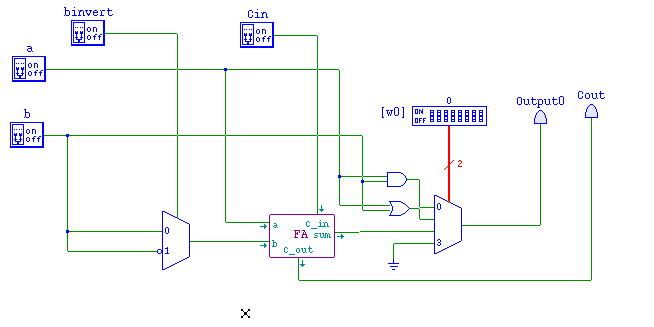
    • Note the new input: Cin
    • And a new output: Cout.
• Observe that subtraction in two's compliment can be accomplished by
  • Flipping the bits and adding 1.
  • Which is just running the second bit through a not gate.
  • And making the carry in a 1 to the first 1 bit ALU
  • So we need another input, BInvert
  • Note that this can be driven by the second bit of the aluop.
  • 
• Finally, we need a nor.
  • But De Morgan comes to our rescue here
  • a + b = a · b
  • Add a AInvert line, this is the msb of the control code.
  • feed the output of both multiplexors to athe and/or, we get a nand for free, what is the control code necessary to accomplish this? .
  • 
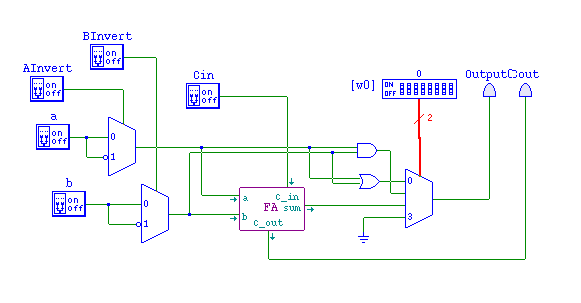
• The implementation file.