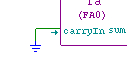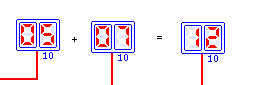A TKGate Lab Exercise

In this project, you will build an 8 bit ripple carry adder. This is based on the discussion in "Computer Science Illuminated, 6^th Edition".

• Start TK-Gate, start a new project (Adder.v).
• Place a comment in your document
  • Right click in the document, select the components sub menu and the comment choice
    • 
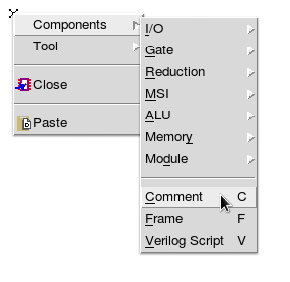
    • I will note this as components->comment
    • Or left click on the canvas and type C
  • Include:
    • Your name
    • Any collaborators.
    • 
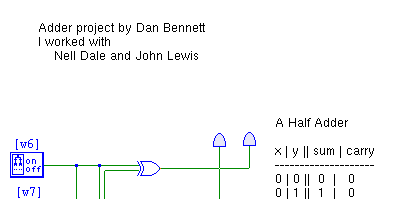
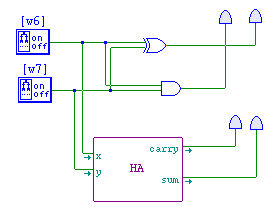
• In the last homework, you built a half adder using gates. Just to review:
  • A half adder computes the sum and carry when two bits are added.
  • For inputs x and y, implement the following formulas
  • sum = x ⊕ y
  • carry = xy
  • (⊕ is the exclusive or (xor) operator)
  • Develop this circuit. We will use it to test the module once we have it built.
  • In a comment, record the truth table for this circuit. (You will need to derive this from the equations or from running the circuit)
  • 
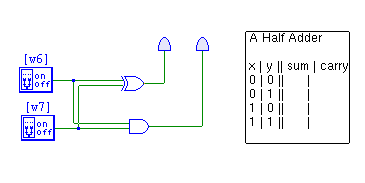
• In tkgate you can build a module, or hardware component.
• Build a half adder module.
  • Select Module, New from the main menu.
  • Enter the title of your module into the Name and select ok. Name this module HA for half adder
  • Click on the Interface tab, and select your module (resize if you wish to make the name fit)
  • Double click on your module to open the Interface Properties menu
    • Add input ports on the left hand side, x and y
      • Remember these names, you will need them when creating the module logic.
      • The names must match exactly later, they are input parameters.
    • Add two output ports on the right side, sum and carry.
      • Remember these names, you will need them when creating the module logic.
      • The names must match exactly later, they are output parameters.
    • You can resize and move the ports on the image on the right.
    • I would build my half adder module with the carry output as the upper output on the right side and the sum on the bottom.
    • 
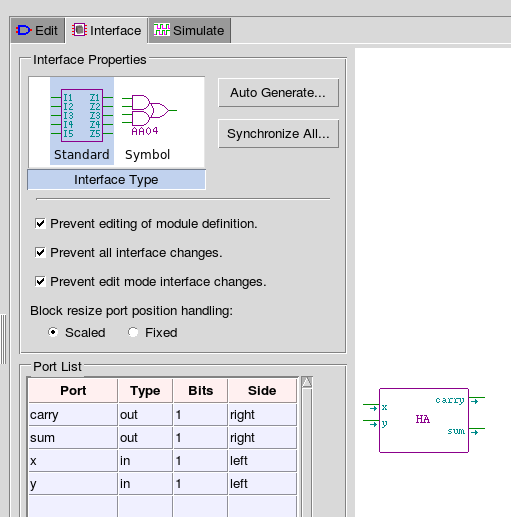
  • Return to the Edit tab and create an instance of your new module
    • Right Click-> components -> modules -> Module Instance -> (select your module)
    • Right click on your module and select open
    • This will give you a blank screen, you are now editing your module.
    • Add two inputs
      • Right Click -> components -> modules -> module input
      • Label the first x, the second y.
      • Note, these must match the input names you gave when creating the interface.
    • Add two output
      • Right Click -> components -> modules -> module output
      • Label the first sum and the second carry
      • Note, these must match the output names you gave when creating the interface.
    • Add a xor and and gate.
    • 
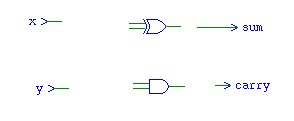
    • Wire the circuit
    • 
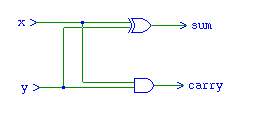
    • Right click anywhere on the blank canvas and select close
  • Wire your module in and test it. The module and the circuit should produce the same output.
  • 
  • After your module is working correctly, return to the Interface tab and lock editing the module interface and definition.
    • 
• Create a Full Adder
  • Unlike a half adder, a full adder takes two bits, and a carry from the previous computation.
    • Remember, the full adder takes three inputs and produces two outputs.
    • By hand, add 23756 + 97289, using the addition algorithm. Write down the carry at each stage. (Yes, I mean on paper with a pen/pencil, or go to the white board and do this as a group)
    • Note how the carry "ripples" through the computation.
    • By hand add the binary numbers 01011 + 01101 using the same algorithm. Write down the carry at each stage.
    • Note the initial carry is 0 in both cases.
    • Note in both cases, we have three inputs to the adder for each addition step.
    • I don't need this paper, it is so you see how a ripple carry adder works.
  • A full adder is built from two half adders.
  • 
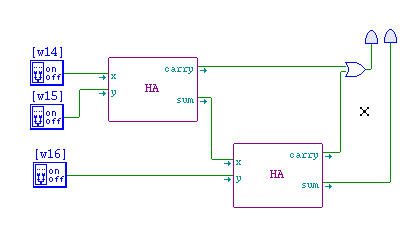
  • At the gate level it would be
    • 
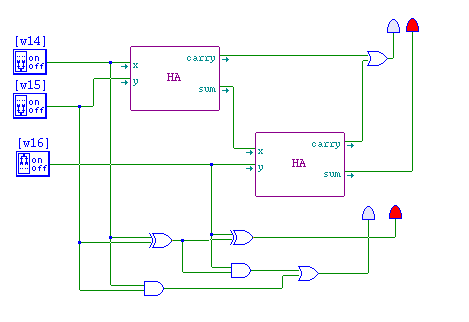
    • carryOut = carryIn ·(x⊕y) + (xy)
    • sum = (x ⊕ y ) ⊕ carryIn
  • Derive a truth table for the full adder.
    • The input will be x,y, carryIn
    • The output will be sum, carryOut
    • Place this in your circuit design as a comment.
  • Build a full adder in two ways
    • At the gate level using and, or, not , xor
    • Using your half adder module and other logic needed.
    • Test your full adders.
  • Build a module to implement a full adder.
    • The inputs should be x,y,carryIn (top to bottom)
    • The outputs should be carryOut, sum (top to bottom)
    • Build a circuit to test your new module
    • 
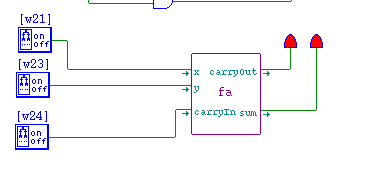
    • Once the module is working, lock the interface.
• Build a 5 bit ripple carry adder.
  • Read the instructions first and LOOK AT THE CIRCUIT BELOW FOR THE FINAL LAYOUT
  • This will consist of five full adders (FA₀ through FA₄)
  • 10 inputs
    • x₀ through x₄, the bits of the first number
    • y₀ through y₄, the bits of the second number
  • 6 outputs
    • sum₀ through sum₄
      • sum_n is the sum of bits x_n, y_n and carryOut_n-1
      • For sum₀, carryIn is 0
    • carryOut, this is the carry out from FA₄
  • Build the ripple carry adder circuit
    • Arrange five full adder circuits vertically.
    • Connect a ground to carryIn from FA₀
      • The ground is components->I/O->ground
      • 
    • Connect carryOut_n to carryIn_n+1
      • 
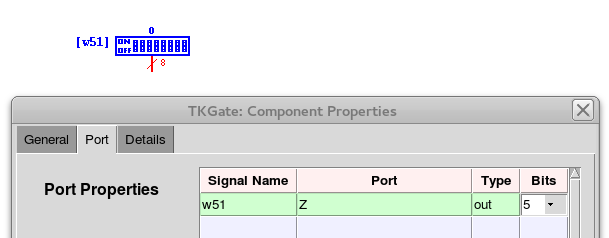
    • Create two DIP switches, and set the port width to be 5.
      • components->I/O->DIP switch
      • Double click on the switch
      • Click on Port
      • Change Bits to 5
      • 
      • I would copy and paste for the second switch.
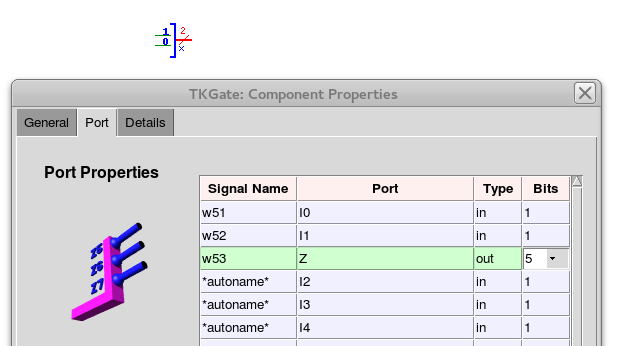
    • Create two concat components, make the Z port 5 bits and add three more ports like I0.
      • A concat component allows us to split a n bit wire into n 1 bit wires.
      • The default is a 2 bit wide wire. But we need a 5 bit wide wire split from the DIP switches above.
      • Get a concat component, components->I/O->concat
      • Double click to bring up the component properties dialog
      • click on I0, then click on Add three times
      • Click on Z, and change the bit width to 5.
      • 
    • Connect x_n, y_n to the corresponding ports on FA_n
    • Create an 6 bit LED bar
    • Create a concat component, make the Z port 6 bits and add four more ports like I0
    • Wire your ripple carry adder as shown
    • 
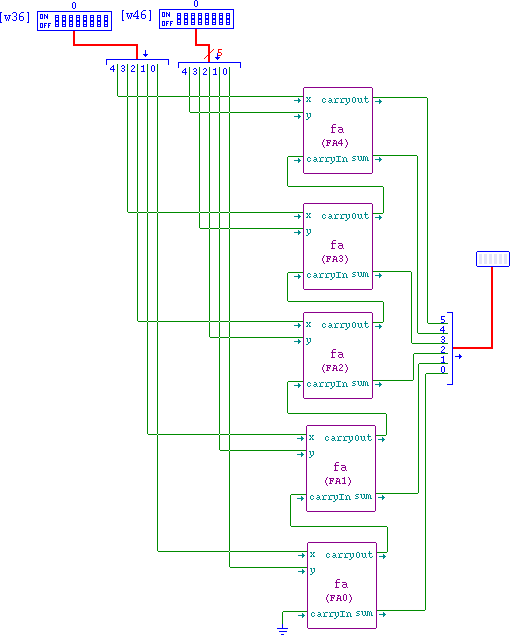
  • Test your circuit to see that it works.
    • Using Decimal based 7-Segment LEDs and comments to display your computations as shown below.
    • 
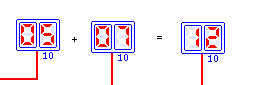
  • Email a copy of the final circuit (a 5 bit ripple carry adder) to your instructor.