The components of computer organization

• There are three basic items we use in our discussions
  • not
  • and
  • or
• They are supplemented with
  • xor
  • nand
  • nor
• I will be using screen shots from CircuitVerse.
• Basic input/output
  • We will represent a power source as a 1.
  • We will represent ground as a 0.
  • We have a input device which can select between the two.
  • We have an output device which will display a 0 or 1 appropriately.
  • We have a Digital LED (light emitting diode) which will glow if a 1 is present or not if a 0 is present.
  • 
  • When you do this in math, they are not worried about power, ground, ...
    • They are worried about true or false.
    • Generally we will use 0 in place of false (F).
    • We will use 1 in place of true (T)
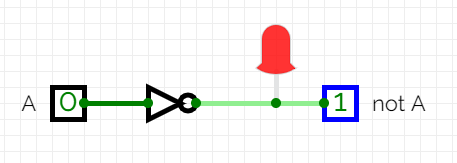
• not
  • This basically inverts or flips the logic.
    • Given a basic statement: Today is Friday.
    • The inversion of that statement is : Today is not Friday.
  • $X = A'$ or $X = \bar{A}$ or $X = \lnot A$.
  • The gate is
    • A triangle on its side with a circle at the point.
    • The input straight edge is the input side.
    • The circle is the output side.
    • Sometimes a not gate is collapsed into a circle.
    • 
  • The truth table
    • This is a single input element, so there is only one column on the left.
    • This is a single output element, so there is one column on the right.
    • The first row is a label, in this case x and x'

    • x	x'

    • We then need to list all possible inputs on the left hand side.
      • Since there is one input, there are $2^1$ possible inputs {0,1}.

    • x	x'
      0
      1

    • Finally we need to fill in the logic on the right hand side.

    • x	x'
      0	1
      1	0

    • If the math people were building this table they would write

    • $x$	$\lnot x$
      F	T
      T	F

• A basic rule:
  • Use the notation that matches the circumstance.
  • Do not demand that you use another notation.
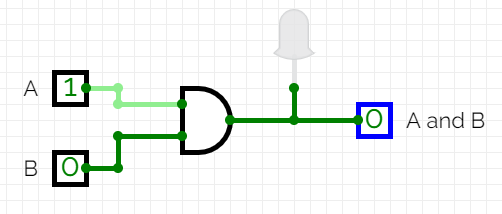
• and
  • This is a two input function.
  • Both elements must be true, or 1 for the result to be true, or 1.
  • Today is Friday and I am in class.
    • This statement is not true if today is not Friday
    • This statement is not true if I am not in class.
  • $X = A * B$, or $X= A \land B$
  • The gate is sort of a D looking thing.
    • The two inputs are on the long side.
    • The output is on the curved side.
    • 
  • The truth table
    • There are two inputs, so there are $2^2$ possible input combinations.

    • A	B	A * B
      0	0	0
      0	1	0
      1	0	0
      1	1	1

• or
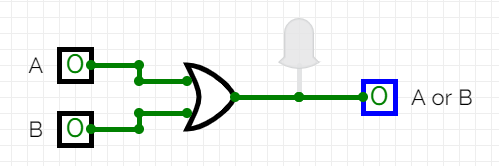
  • If either statement, or both statements, are true, then the resulting statement is true.
  • Today is Friday or I am in class.
    • The statement is true if it is Friday
    • The statement is true if I am in class.
    • The statement is true if it is Friday and I am in class.
  • This is sometimes called the inclusive or.
  • $X = A + B$ or $X = A \lor B$.
  • The symbol
    • 
  • The truth table

    • A	B	A + B
      0	0	0
      0	1	1
      1	0	1
      1	1	1