Ciruits

• Circuits are a combination of gates.
• A combination circuit is a circuit whose output is soley determined by the input values.
  • These will be most of the circuits we build today.
• A sequential circuit is a circuit whose output is a function of the input and the current state of the circuit.
  • These are memory circuits and will be discussed later.
• I always had problems with this section because they just seemed to "Introduce" circuits.
• There is a method to get started.
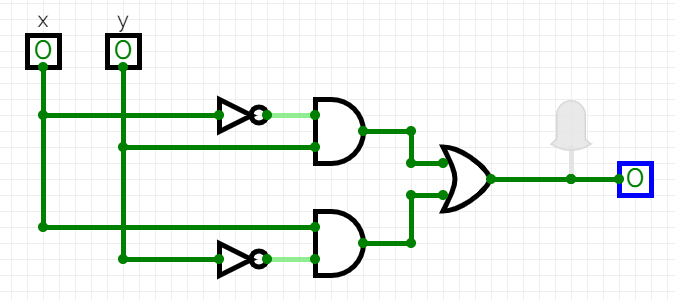
  • I would like to build a circuit for the xor function.

  • x	y	$x \oplus y$
    0	0	0
    0	1	1
    1	0	1
    1	1	0

  • Note the two rows where there is a 1 in the output.
  • Write the expression that would make these true
    • x = 0, y = 1 could become x'y
    • x = 1, y = 0 could become xy'
  • Note that the circuit is an or of these two.
  • $x \oplus y$ = x'y + xy'
  • We can now turn this into a circuit
    • 
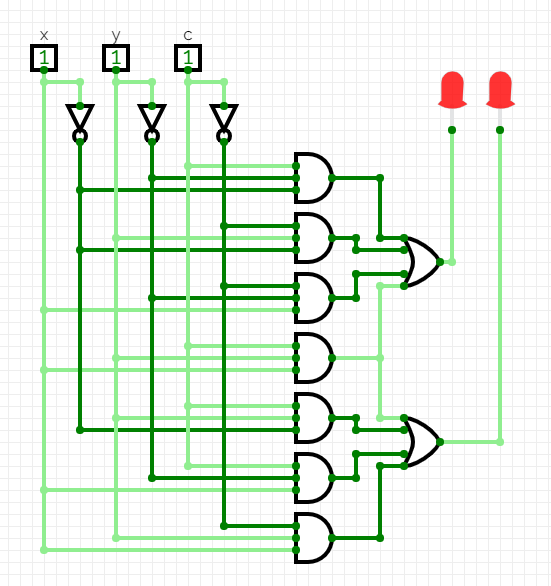
• How about building something that will add three bits.

  • x	y	c	s	c
    0	0	0	0	0
    0	0	1	1	0
    0	1	0	1	0
    0	1	1	0	1
    1	0	0	1	0
    1	0	1	0	1
    1	1	0	0	1
    1	1	1	1	1

  • s = x'y'c + x'yc' + xy'c' + xyc
  • c = x'yc + xy'c + xyc' + cyc
  • A save file of the circuit adder.cv
  • 
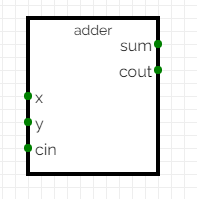
  • If we package this up, we can build a single bit adder
  • 
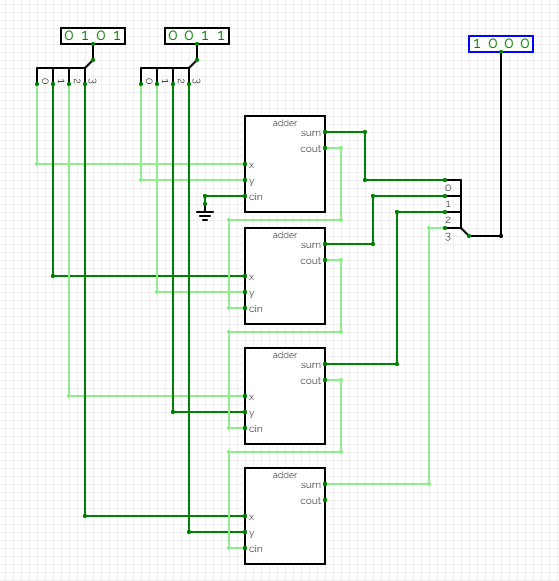
• Connecting the cary out of one of these to the cary in of another gives s the ripple carray adder
  •