Representing Data, Some Ideas

• So we have the basics of binary down.
  • This will do for positive integers.
  • But what about other data?
• A quick discussion of data vs information
  • Data is basic values or facts.
  • Information is data that has been organized or processed in a useful manner.
  • Data is somehow raw as opposed to information which has probably been processed.
• We will look at different types of data
  • Numbers: integers, signed integers, real numbers.
  • Text: letters and more
  • Audio data: briefly
  • Images and Graphics: again briefly
  • Video: very quickly
• I don't care too much about compression at this stage.
• Analog vs Digital
  • We believe that we live in a continuous world.
  • Therefore we can have continuous data.
  • We call this analog data.
  • However computers are definitely not continuous.
  • In this world, we represent data in a discrete manner.
• What?
  • Take a paint brush with two different colors of paint on the sides.
  • Blend this across the page.
  • There will be MANY MANY different colors, smoothly transitioning between the two colors
  • (https://www.thesprucecrafts.com/how-to-blend-paint-colors-2578066)
  • This is analog.
  • In the digital world, we might represent
    • brown as $CC6E10_{16}$ (204, 110, 16)
    • yellow as $E6BC5A_{16}$ (230, 188, 90)
    • See This app.
    • Or there are about
      • 26 steps of red between the two
      • 78 steps of green between the two.
      • 74 steps of blue between the two.
  • Frequently we discuss the difference as position vs numbers.
    • Think about a thermometer.
      • On an analog thermometer you judge the temp by position.
      • If you can read it more accurately, you can get more levels of precision.
      • But on a digital thermometer, you only get the digits provided.
  • Digitize: the act of converting analog information to digital.
  • Why Digital? Why Binary?
    • This is an idealized representation of two signals
    • 
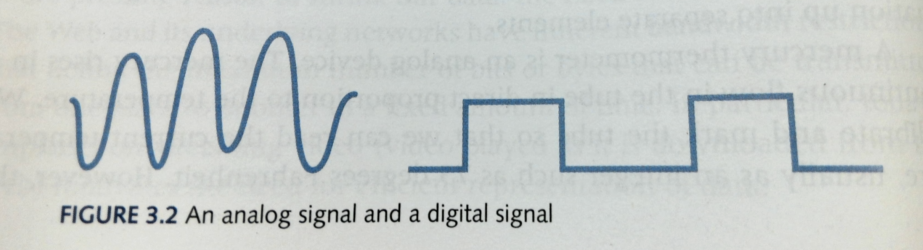
    • In the "digital" signal, it is easy to differentiate the two different values.
    • Even in the case of signal degradation.
    • 
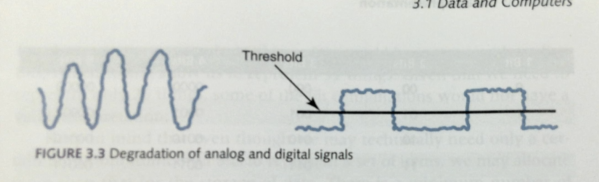
  • Number of digital representation.
    • If I want to give a binary code name to two people, how many digits do I need?
    • How about 4?
    • Is there a pattern here?
    • If I have $n$ binary digits, I can name, or encode, $2^n$ things.
    • Look at the different permutations of 3 bits, 4 bits, ...
    • In the other direction if I have $k$ things to represent I will need $n = \lceil \log_2k\rceil$ bits.
      • If $k = 2^n, \log_2k = n$