Gray Code

• Invented by Frank Gray (among others)
• This is a code that is used for
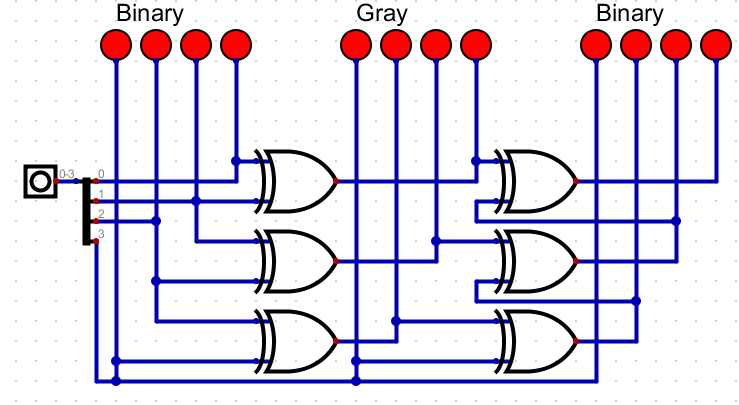
  • Error minimization, Error Detection
  • Error free data transmission.
  • Analog to digital conversion.
  • Representation in genetic algorithms.
  • Circuit design
• We are learning it for the last point.
• It is called a reflective code, because the top and bottom halves of a gray code table are "reflections"
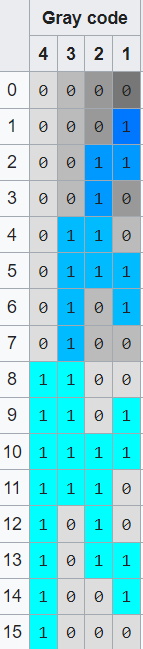  • (wikipedia)
• The goal is each successive "number" differs by 1 bit.
  • A two bit gray code: 00, 01, 11, 10
  • Three bit gray code: 000, 001, 011, 010, 110, 111, 101, 100
  • Four bit Grey code: 0000, 0001, 0011, 0010, 0110, 0111, 0101, 0100, 1100, 1101, 1111, 1110, 1010, 1011, 1001, 1000

    Value	2 bit	3 bit	4 bit	binary
    0	00	000	0000	0000
    1	01	001	0001	0001
    2	11	011	0011	0010
    3	10	010	0010	0011
    4		110	0110	0100
    5		111	0111	0101
    6		101	0101	0110
    7		100	0100	0111
    8			1100	1000
    9			1101	1001
    10			1111	1010
    11			1110	1011
    12			1010	1100
    13			1011	1101
    14			1001	1110
    15			1000	1111

• If we are stepping through the nubers 0-15, we might encounter a problem changing from 3 to 4.
  • 3 = 0011₂
  • 4 = 0100₂
  • We need to turn off switches 0, and 1 and turn on switch 2.
  • But these don't all happen at once,
  • So we might go through the patters 0011->0010->0000->0100
  • And this will cause sperious input
• In gray code, this is less of a problem, as we will only toggle one switch to go from 3 to 4
  • 3 = 0010_gray
  • 4 = 0110_gray
  • Only a single switch is changed, no state transistion.
• Conversion to and from binary.
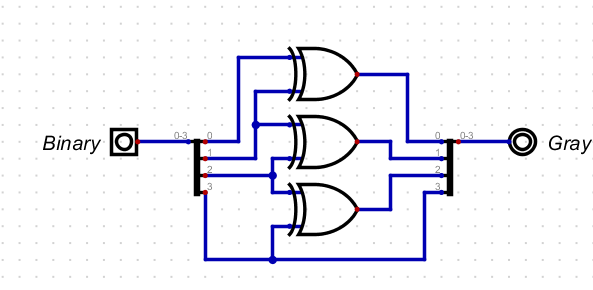
  • To convert from binary
    • The MSB is the same
      • G_msb = B_msb
    • Every other bit xor with the previous binary bit.
      • G_n-1 = B_n ⊕ B_n-1

    • Convert 13 to gray code
      11012 = 
          G3 = B3 = 1
          G2 = B3 ⊕ B2
             = 1  ⊕ 1 = 0
          G1 = B2 ⊕ B1
             = 1  ⊕ 0 = 1
          G0 = B1 ⊕ B0
             = 0  ⊕ 1 = 1
             = 1011gray
      
      Convert 10 to gray code
      10102 
          G3 = B3 = 1
          G2 = B3 ⊕ B2
             = 1  ⊕ 0 = 1
          G1 = B2 ⊕ B1
             = 0  ⊕ 1 = 1
          G0 = B1 ⊕ B0
             = 1  ⊕ 0 = 1
             = 1111gray 

  • 
• Convert from Gray to Binary
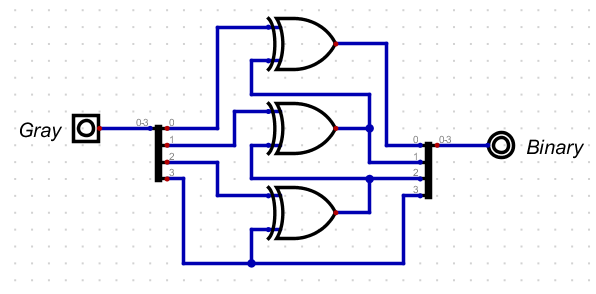
  • B_MSB = G_MSB
  • B_n-1 = B_n ⊕ G_n-1

• Convert 1001gray to binary
  1001gray = 
      B3 = G3 = 1
      B2 = B3 ⊕ G2
         = 1  ⊕ 0 = 1
      B1 = B2 ⊕ G1
         = 1  ⊕ 0 = 1
      B0 = B1 ⊕ G0
         = 1  ⊕ 1 = 0
         =  11102 

• 
• the digital file

Supplimental Note

• The table and the circuit above are correct.
• I tested them with:
• 
• this file