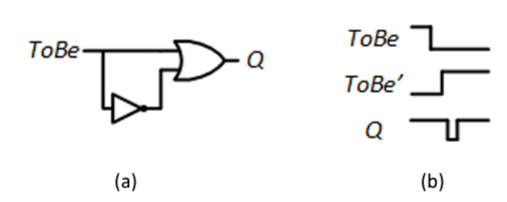AND and OR

• For us, the next two most basic operations are and and or
• and
  • Both inputs must be true for the circuit to be true.
  • expression: f(a,b) = ab or f(a,b) = a ∧ b
  • Truth table
    • There are 2 inputs, so there should be $2^2=4$ rows

    a	b	ab
    0	0	0
    0	1	0
    1	0	0
    1	1	1

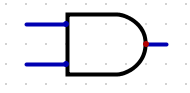
  • Symbol:
  • 
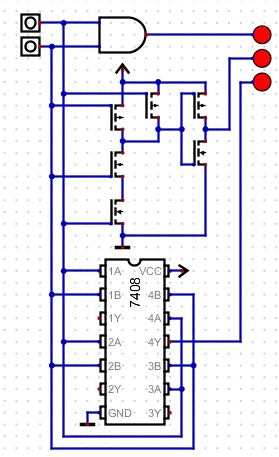
  • digital circuit
  • Please note, my transistor circuit is not optimized.
• or
  • One or the other or both.
  • Sometimes called the inclusive or.
  • f(a,b) = a+b, f(a,b) = a ∨ b

  • a	b	a+b
    0	0	0
    0	1	1
    1	0	1
    1	1	1

  • 
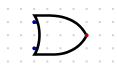
  • If your handwriting on a test is sloppy, put a + in the middle of an or gate.
• I generally work with these three gates, not, and, or.
  • It matches the way I think.
  • And it is the logic we use at the programming level.
  • But there are more.
• xor
  • Exclusive or
  • One or the other but not both.
  • f(a,b) = a ⊕ b

  • a	b	a⊕b
    0	0	0
    0	1	1
    1	0	1
    1	1	0

  • 
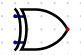
• nand
  • not and.
  • f(a,b) = ab

  • a	b	ab
    0	0	1
    0	1	1
    1	0	1
    1	1	0

  • It is my understanding that
    • Nand requires fewer transistors than and
    • It is one of the tools electrical engineers, computer engineers, ... work with.
• nor, xnor
  • Again, these potentially require fewer transistors.
  • So they are commonly used.
• Interestingly nand and nor are universal
  • This means that all other logic gates can be built from them.
• More than two input gates exist.
  • In general they extend the function.
  • A three input and gate requres all three inputs to be true for the output to be true.
  • A three input or gate requres one or more input to be true for the output to be true.
  • A three input xor gate requires exactly one input to be true for the output to be true.
• At the end of chapter 3, Carpinelli discusses practical limitations on gates
  • We can design equations, and even digital circuits that we really can't implement.
  • Fan-in
    • For a gate, this is the maximum number of inputs it can support.
    • The more inputs the slower the gate.
      • Because there are more transistors requred to accomplish thetask.
      • And they can not all operate in parallel.
    • Depending on the technology the practial limit is between 2 and 8 inputs.
    • For 3100, we will sort of ignore this.
    • For 2100 we will work on solutions.
    • But an 8 input and gate can be accomplished with 2-4 input and 1 normaland gates.
    • 
    • the digital file
  • Fan-out
    • This is related to the number of other gates that can be connected to the output of a single gate.
    • The gate will not produce enough current to drive the connected gates when the number is too high.
    • Again depending on technology this can be as low as 4 or as high as 50.
    • Again, 3100, don't worry, 2100 we will do some fixes.
  • Propogation Delay
    • Each transistor takes some time to switch.
    • Generally we idealize ths to be
      • Not has a propogation cost of less than 1
      • And and Or have a cost of 1 (this should probably be nand and nor)
      • Others have a cost of 1 or more.
    • We can demo this in Digital
      • The Data Graph (under I/O) is helful here.
      • Make sure to label all input and output.
      • And enable Show single gate steps in the graph
      • 
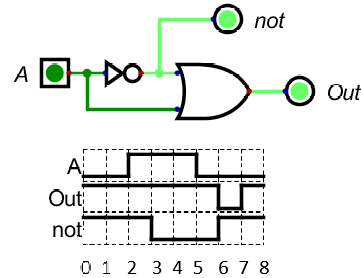
      • This circuit should always produce a 1.
        • At time 0, A is low, and the output of the circuit is high.
          • Sometimes the circut shows out as low for a time step
        • At time 2 the circuit has stabalized in the simulation, so the user switches a from Low to High.
        • At time 3 (note the delay) not goes low.
        • At time 5 the circuit has again stabalized in the simulation, so the user switches A from High to Low
        • Note the the not raises to high at step 6
        • At the same time, the not was producing a low and A was low so the or gate produces a low for a "time step"
        • At time 8 the circuit has stabalized.
    • This would not look like this "in the real world"
      • The steps would not all be the same size.
      • And they would be curves, not steps.
    •