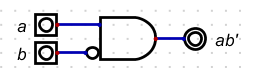
$\require{cancel}$
Circuits, Truth Tables and Equations
- This is from Carpinelli chapter 2.
- In L&S we will deal with this in more depth.
- Given an equation, we can "prove" it with a truth table.
- This is a form of exhaustive proof which is possible because of the limited set of inputs.
- show ab = ba
| a | b | ab | ba |
|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
- As a side a=b is the same as nxor
| a | b | a=b | a⊕b | a⊕b |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 1 |
- We can build a circuit to test this
-
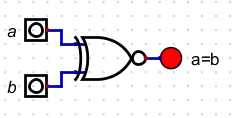
- So we could build a circuit to test our original property.
-
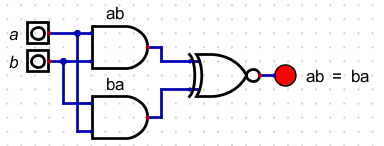
- Note, when we test this circuit, it never turns off, which is what we want.
- I a math class (discrete I think) you will do more with boolean algebra
- Let's look at the expression f(a,b) = ab
- Can we form a circuit for this expression
- Can we create the truth table.
- We will do this by building a row for each of the simple terms of the expression.
- Iin this case, the only term is b
| a | b | b | ab |
|---|
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
- Does a·b = a·b?
- Build the truth table.
- Build the circuit.
- Note this is one part of DeMorgan's Laws.
- you can use an equation to produce a truth table or a circuit.
- You can also read an equation from a circuit.
- You can use a truth table to verify a circuit matches an equation.
- Or the other way around.
- Circuits for this section.