$\require{cancel}$
Minterms
- Our ultimate goal is to have sufficient skills to build circuits to accomplish our tasks.
- Frequently we will start with a truth table.
- Two input problems are trivial
- So we will move to three input problems.
- I have a board of three, I want a circuit to detect when a majority vote is achieved.
- So I want the circuit to light up when two or more of the board votes.
- We can assume that they will vote by pressing a button.
- We could mess around and try to build a circuit but let's start with a truth table.
- There are 3 inputs, so $2^3=8$ rows.
-
| a | b | c | Pass |
|---|
| 0 | 0 | 0 | |
| 0 | 0 | 1 | |
| 0 | 1 | 0 | |
| 0 | 1 | 1 | |
| 1 | 0 | 0 | |
| 1 | 0 | 1 | |
| 1 | 1 | 0 | |
| 1 | 1 | 1 | |
- In chapter 2, Carpinelli discusses Sum of Products (page 2-13)
- We will discuss thoroughly in Logic and Switching Theory
- We will casually discuss this now in both.
- Given a truth table, we can build an equation by looking at the terms that have a final value of 1.
- these are called the minterms.
-
| a | b | c | Pass |
|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
- Consider a=0, b=1 and c=1.
- f(0,1,1) = 1 if
f(0,1,1) = 0 · 1 · 1
- What is the output of f(a,b,c) = abc?
- We could build a truth table:
-
| a |
b |
c |
a |
ab |
(ab)c) |
| 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 |
- Write the similar expressions for the other minterms.
- If we add those together we get
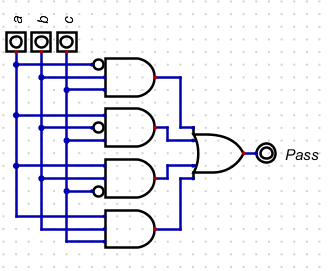
- f(a,b,c) = abc + abc + abc + abc
- From this we can build a circuit
- Build a circuit that detects when any two vote against.
- In Logic and switching we will discuss methods to optimize these circuits.