$\require{cancel}$
Building an Adder
- Let's quickly review base 10 addition.
- Perform the following 215+206
- What is the algorithm?
- What is a carry?
- For a number position we will distinguish carry in and carry out.
- What is the sum at a number position?
- In base 10, what is the maximum carry?
- In base two, the addition table is much easier.
-
- It is useful to know/remember in binary 1+1+1 = 11.
- Add $11010111_2 + 11001110_2$
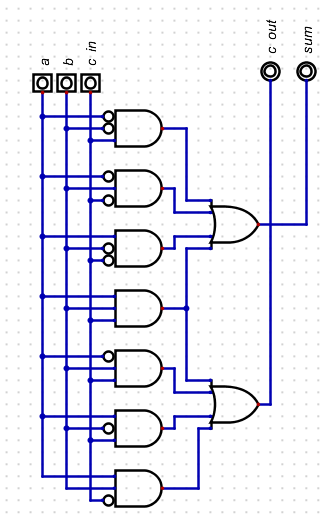
- Can we build a table to represent the addition of two bits and a carry in?
| a | b |
cin |
c out |
sum |
|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
- Construct the minterms
- sum = a·bc
+ abc
+ ab·c
+ abc
- c out = abc
+ abc
+ abc + abc
- Build and test the circuit
- There are optimizations of this circuit. In 2100 they will learn how to do this.
- But for us, this will do.
- By the way, you if you use only inputs and outputs for data sources you can use the circuit as a module.
- It shows up in the custom library.
- You might need to reorder the inputs/output
- Wide Input and output
- Changing the number of data bits on input/output will allow you to input/output larger numbers.
- Under wires a splitter/merger will allow you to split these into individual bits.
- Using the full adder we built before, let's build a four bit ripple carry adder
- We will hard wire the 0 bit carry in to be 0
- We will allow the carry to ripple between adders by wiring the
carry out of a lower bit to the carry in of the next bit.
-
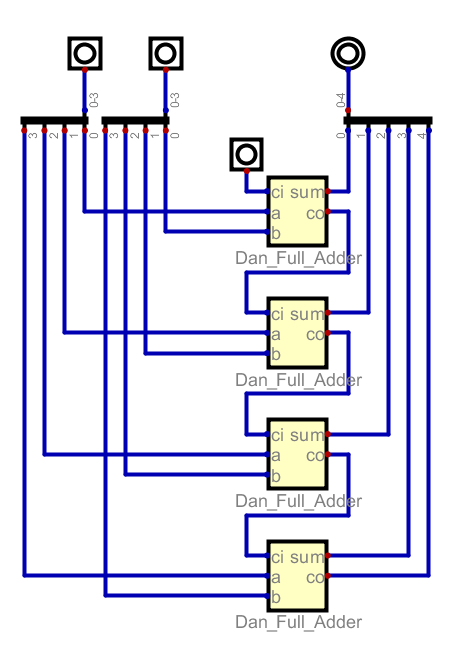
- digital file. (you need Dan_Full_Adder.dig from above in the same directory.
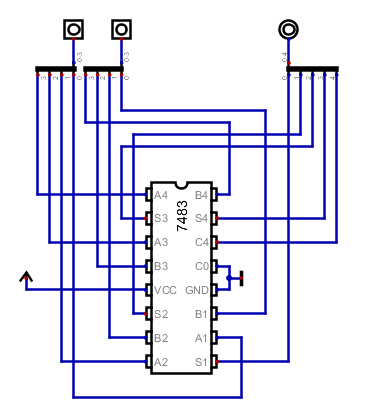
- The 74283 family of chips implement a four bit adder