Subtraction and Two's Complement

• How do we represent negative integers?
  • The method is called sign magnitude.
  • The magnitude is the distance from 0 and the sign is the direction.
  • Think -7 and +7.
  • We normally do not write down the + sign for positive numbers.
• Note in a given precision adding negative numbers
  • Requires a bit to represent the sign, say 0 for + and 1 for -
  • But this reduces the range of numbers.
• Think 3 bits.
  • We can produce $2^3 = 8$ different bit patterns.

    Pattern	Signed	Unsigned
    000	0	0
    001	1	1
    010	2	2
    011	3	3
    100	-0?	4
    101	-1	5
    110	-2	6
    111	-3	7

  • We can represent 8 unsigned numbers
  • We can represent 7 signed numbers because -0 = 0!
• -0 is the first problem with sign magnitude
  • We waste a bit pattern
  • We need to build our algorithms to deal with a -0
• How do you perform the following subtractions (by hand)?
  • 34 + 27 : just add
  • 34 - 27 : just subtract
  • -27 + 34: turns into 34 - 27
  • 27 - 34 : note that 34 is "bigger" so subtract 27 from 34 and make the result negative
  • -34 + 27 : is the same as above
  • -27 - 34 : note the signs are the same so add and keep the -
  • -27 - -34 : note the signs are different, rewrite as 34 - 27
  • We do this autmoatically (I think)
  • But we have different rules based on the mix of signs.
• Jorgensen notes that we need typing in a language because (in our example) what does 101 represent? -1 or 5!
• Two's complement
  • The wikipedia article on two's complement is not bad.
  • Jorgensen is very breif.
  • This is a way to represent negative numbers.
  • It makes signed addition/subtraction a single operation.
  • And conversion is simple.
  • Note two's compliment requires a fixed bit size.
• The two's compliment of a number is its negative.
• To form the two's complment of a number
  • Flip the bits - ie change all 0 to 1 and 1 to 0
  • add 1
• Let's explore 3 bit two's compliment
  • 000 -> 111+1 => 000, the compliment of 0 is -0
  • 001 -> 110 + 1 => 111
    • 111 + 001 = 1000 we discard the carry of 1 so -1 + 1 = 0
  • 010 -> 101 + 1 => 110
    • 010 + 110 = 1000 agan discard the carry of 1.
  • 011 -> 100+1 -> 101

  • pattern	meaning
    000	0
    001	1
    010	2
    011	3
    101	-3
    110	-2
    111	-1

  • Note that the msb indicates the sign
    • A msb of 0 is positive
    • A msb of 1 is negative
    • It is not a sign bit, it is an indicator.
  • The only thing missing is 100
    • It must be negative, the first bit is 1
    • Find out the magnitude take the two's compliment
    • 100 -> 011+1 -> 100 aaarrgghh
    • Let's try a little math
    • 100 + 001
      • (?+1) = 101
      • 101 -> 010 + 1 => 011
      • 011 = 3 so 101 = -3
      • So ?+1 = -3, ?=-4
    • Let's try a few more
      • 010 + 100 = 110 -> 001+1 => 010, so ?+2 = -2, ?=-4
      • 011 + 100 = 111 -> 000+1 => 0l1, so ?+2 = -1, ?=-4
    • So 100 is -4, there is no positive 4.
  • But remember, we said for n bit sign magnitude numbers the range is $-2^{n-1} to 2^{n-1}-1$
    • So for 3 bits, $-2^{3-1} to 2^{3-1}-1$
    • Or -4 to 3
  • Let's investigate 4 bit two's complement
    • The range is $-2^{4-1} to 2^{4-1}-1$ or -8 to 7
    • With for bits we can represent $2^4 = 16$ different things.
      • Is this an efficient use of the bits?

    • pattern	meaning
      0000	0
      0001	1
      0010	2
      0011	3
      0100	4
      0101	5
      0110	6
      0111	7
      1000	-8
      1001	-7
      1010	-6
      1011	-5
      1100	-4
      1101	-3
      1110	-2
      1111	-1

    • Convince yourself the table is right.
• Can we build a circuit to subtract two's complement numbers?
  • We want to compute a-b
  • To do this we want to add a+b' where b' is the 2's compliment of b.
  • To find b', we flip the bits and add one.
  • So we can just not b to flip the bits.
  • And set the initial carry in to be 1 to add one.
  • 
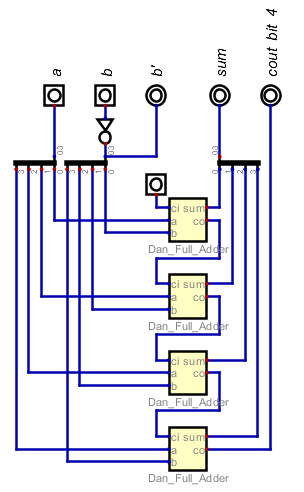
  • subtract.dig, needs Dan_Full_Adder.dig in the same directory.