Finishing the ALU

• I am taking this from Patterson and Hennessy
  • They spend quite a bit of time developing this.
• For a simple mips machine we need
  • Add and subtract
  • And, or, a + b (nand), a · b(nor)
  • And a < b
• So they develop an 1 bit alu
  • 
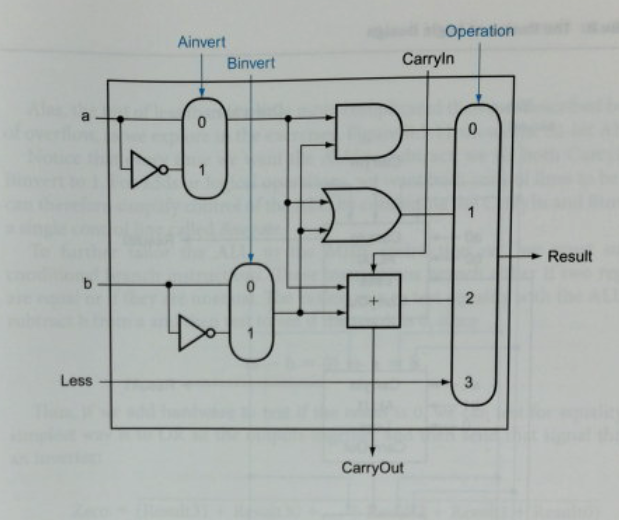
  • There are four data lines
    • a, b, caryin as we have discussed
    • Less is for <
      • We want a 1 if a < b
      • We will subtract, and bring the MSB of the result back.
      • We will see this in a minute.
  • There are three control lines.
    • Ainvert is a one bit line to invert the a bit.
    • Binvert is a one bit line to invert the b bit.
    • Operation is a two bit line to select the output.
  • There are two output lines
    • The one bit result selected by the operation
    • A carry out
• The ALU for the MSB is a bit different
  • 
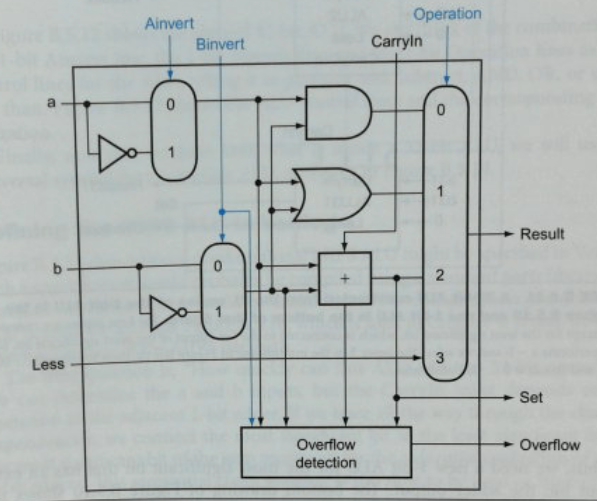
  • Note the overflow detection hardware
    • The rules for two's complement are easy

      Operation	A	B	Overflow?
      A+B	+	+	negative result
      A+B	-	-	0 or positive result
      A+B	-	+	Not possible
      A+B	+	-	Not possible
      A-B	-	-	Not possible
      A-B	+	+	Not possible
      A-B	-	+	0 or positive result
      A-B	+	-	negative result

  • Plus the "set bit" which is the MSB of any computation.
    • Again, if we subtract and the first was smaller, we will have a 1 here.
• Putting it together, we have
  • 
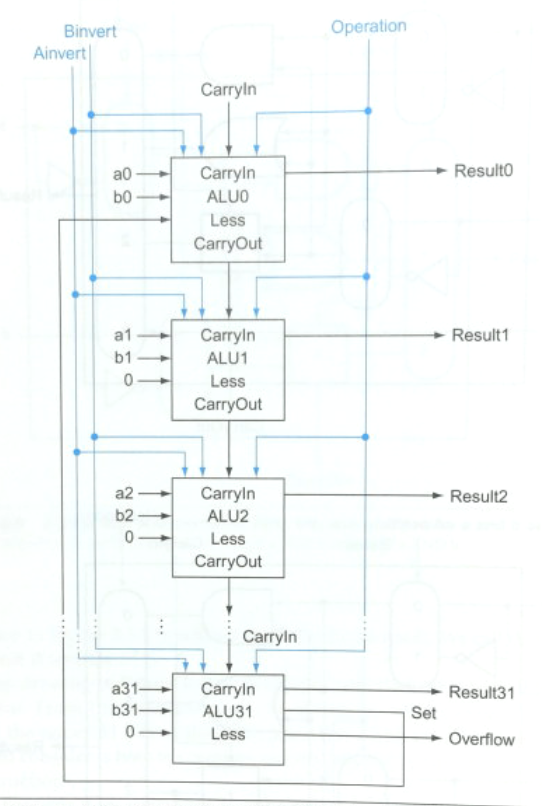
  • The set bit from the last ALU becomes the less bit for the first.
  • All other less bits are 0.
• Note, we could control this from the CU with the following

  • Ainvert	Binvert	Operation	Function
    0	0	00	(0000) and
    0	0	01	(0001) or
    0	0	10	(0010) add
    0	1	10	(0110) subtract
    0	1	11	(0111) less
    1	1	00	(1100) nor
    1	1	00	(1101) nand