Multiplexers

• I am using Kann (sort of) as a reference for this section.
• We would like to build an alu, not just an adder.
• The first problem is we need to have two different inputs to the second feed of the adder.
  • When we are adding, we input b
  • When we are subtracting, we input b'
• We need to design a circuit that will allow us to select between two different inputs.
• For right now, we want to have two inputs, and select between these.
• Fortunately such a circuit exists. (it is called a Multiplexer or mux)
  • Two inputs on the right.
  • One input below to control which of the others inputs is passed through.
  • 
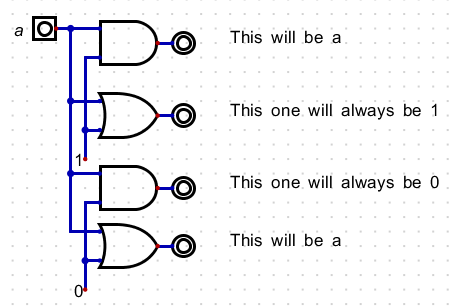
• We need some rules from boolean algebra to build this at the gate level
  • 0+n = n
  • 1×n = n
  • 1+n = 1
  • 0×n = 0
• So If I want to pass something through
  • Or it with a 0
  • And it with a 1
• And If I want to stop something
  • Or it with a 1, I will get a 1 regardless
  • And it with a 0, I will get a 0 regardless
• 
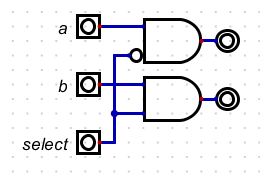
• The first step is how do we select an input?
  • The and seems a good method
  • Let's and an input with the selector, and an input with the not of the selector.
  • 
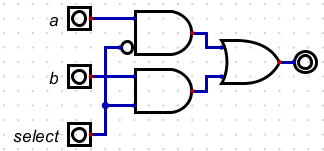
• We can now combine this with the or rule
  • Note one will pass through.
  • The other will be a 0
  • 0+n = n
  • 
• Later we will need to select between more input values
• If we have $2^n$ bits, how many control or selection lines would we need?
• We will need n lines.
• Let's build a 8 input mux.
  • I will need 3 control lines since $8 = 2^3$.
  • 
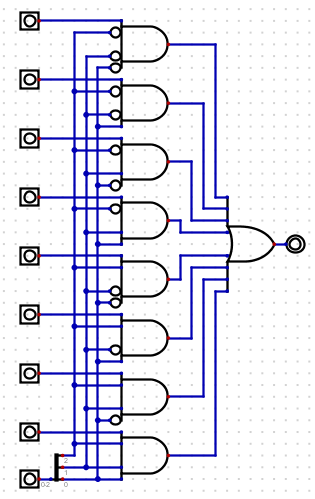
• There is no problem making the wires "thicker"
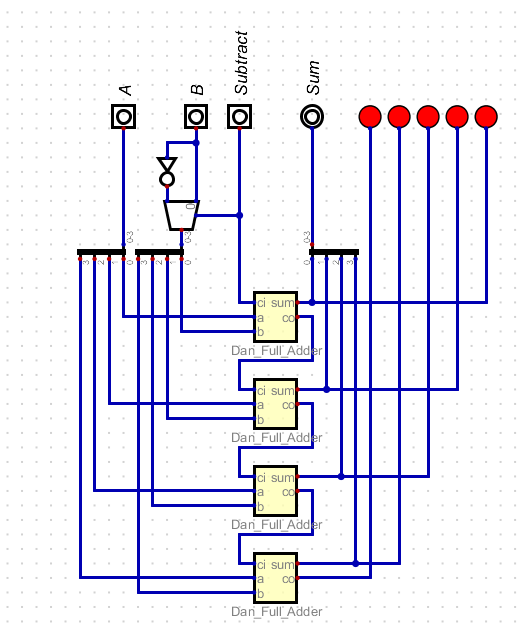
• Build a Add/Subtract Circuit.
  • The carry in now controls a mux.
  • This selects between b and not b.
    • On a 1 not b is selected.
  • I pulled the last carryout bit out of the sum output.
  • And added some leds so we can see the sum bit pattern as well.
  • 
• All circuits digital file, this file is required in the same directory.