Some Examples

• Check Yourself, page 53.

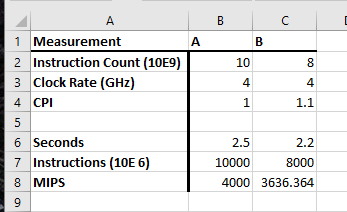
  Consider the following performance measurements for a program:
  
   Measurement
  Computer A
   Computer B
   Instruction Count
   10 billion
   8 billion
   Clock Rate
   4 GHz
   4GHz
   CPI 
   1.0
   1.1
  
  
   Which computer has the higher MIPS rating?
   Which computer is faster?
  

  • To answer part a, we need to know that MIPS is millions of instructions per second.
  • For each machine:
    • Calculate the total time in seconds.
    • Calculate the number of millions of instructions.
    • Divide
  • Generic Derivations
    • For Time in seconds:
      • I have: instructions, clock speed, CPI
      • I want: seconds
      • $\text{seconds} = \frac{\text{seconds}}{ x \text{cycles}} \times \frac{y\text{cycles} }{ \text{instruction}} \times z\text{instructions} = \frac{yz}{x}$
    • For millions of instructions
      • I have: billions of instructions ($10^{9})$
      • I want: millions of instructions ($10^6)$
      • Multiply by $10^3$
  • I set up a spreadsheet to do the actual computations:
    • 
    • 
  • Interpretation: Computer A has a faster MIPS rating on the program, it does more instructions in a second than computer B.
  • However, computer B finishes the program in less time, so it is faster.
  • Please note, I believe that ALL of the above is important for an answer. Simply providing the last two lines, even if your answer is what I have written, is not a satisfactory answer. All portions are required.
• Example 2, Check Yourself page 40:

  • A given application written in Java runs 15 seconds on a desktop processor.
    A new Java compiler is released that requires only 0.6 as many instructions
    as the old compiler.  Unfortunately, it increases the CPI by 1.1.  How fast 
    can we expect the application to run using the new compiler?  

  • Again I want Seconds:
  • $\text{seconds} = \frac{\text{seconds}}{ x \text{cycles}} \times \frac{y\text{cycles} }{ \text{instruction}} \times z\text{instructions} = \frac{yz}{x}$
  • The problem is we don't know the clock speed or the instruction count.
  • So let $i$ be the instruction count of the original program.
  • Let $s$ be the clock speed of the original program.
  • While not stated, assume the original CPI is 1.
  • Original time $15 = t_{old} = \frac{1\times i}{s}$
  • We know the new instruction count is $0.6 \times i$
  • So the new time is $t_{new} = \frac{0.6i \times 1.1}{s} = 0.6 \times 1.1 \times \frac{i}{s}.$
  • But $t_{old} = 15$
  • $t_{new} = 0.6 \times 1.1 \times 15 = 9.9 \text{seconds}$
  • This is answer b.
• Again, simply stating b is an insufficient answer. I wish to see all of your work. Even if you can do it "in your head".
• Presentation options
  • Remember, your work must be typed.
  • So how will you present your homework?
    • Word has an equation editor.
    • So does open office/libre office
    • Latex/Tex is also an option.
      • You can view my mathjax expressions, which are essentually latex, in the source code.
  • Yes it is a pain, look at the source code for the last four sets of ntoes.