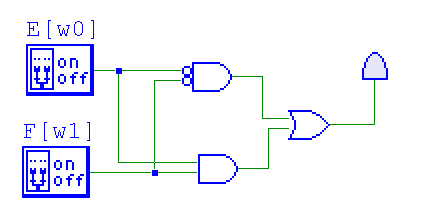
- Create the circuit?
- Create the truth table?
- And has higher precedence than or.
-
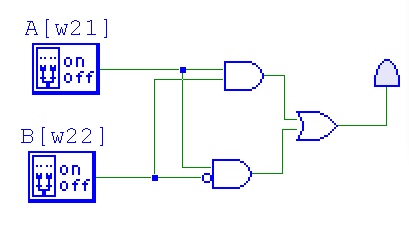
-
$A$ $B$ $AB$ $\overline{B}$ $A\overline{B}$ $ AB + A\overline{B}$ 0 0 0 1 0 0 0 1 0 0 0 0 1 0 0 1 1 1 1 1 1 0 0 1
- On page B-696 they give us several laws of boolean algebra.
-
$ f(A,B)$ $= AB + A\overline{B} $ $= A(B + \overline{B}) $ $= A(1) $ $ = A $
- $\overline{AB} = \overline{A} + \overline{B}$
- $\overline{A + B} = \overline{A} \cdot \overline{B}$
- Pick one, prove it by truth table, prove it by circuit.
-
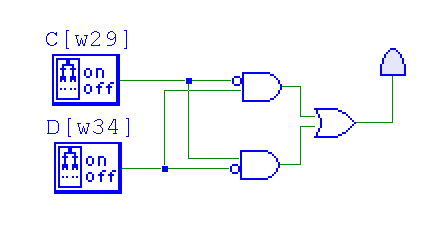
- By the way, this is exclusive or (xor) $C \oplus D$
| E | F | f(E,F) |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
-
G H I f(G,H,I) 0 0 0 0 0 0 1 1 ($\overline{G}\overline{H}I$) 0 1 0 0 0 1 1 0 1 0 0 1 ($G\overline{H}\overline{I}$) 1 0 1 1 ($E\overline{H}I$) 1 1 0 0 1 1 1 1 ($GHI$)