Building an ALU

• This is section B.5 page 716
  • You should read it.
• They assume we have done a better job of looking at the instruction set so:
  • Go to the green card.
  • Look at the CORE instruction set
    • This is not the full instruction set, but it is represetative of the instruction set.
    • The full set is in A.10 (I think)
  • This is also only integer.
  • What MATH instructions do you see
    • Add*
    • OR, NOR, AND
    • Subtract*
  • Could these use the ALU?
    • Branch on *
    • Set Less Than *
• It looks to me like we will problably need an ALU to do all of these.
• We are not going to do chapter 3.
  • it is fantastic, but we don't have time.
  • It covers multiply, divide and floating point.
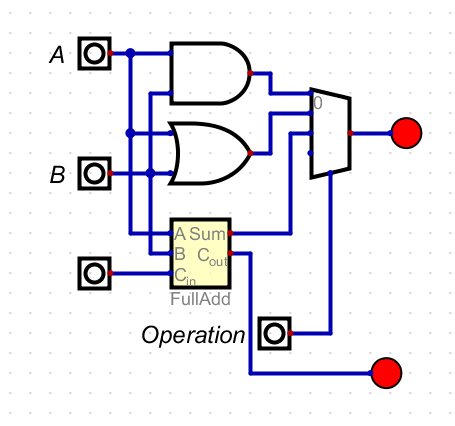
• I like the development of the ALU. It is resonably gentle.
• First they develop a one bit AND/OR unit
  • This has two input bits and produces an and or an or of these.
  • And it has a control line to select which is produced.
  • 
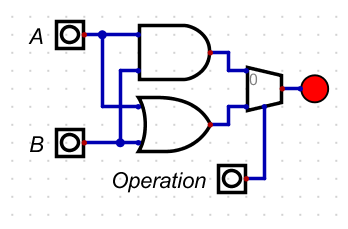
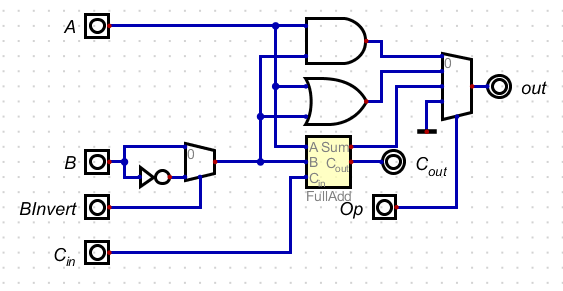
• Next let's develop a full adder.
  • This circuit takes two input bits and a carry in.
  • It produces the sum and a carry out.
  • Build the table
  • Build the expressions
  • Build as a New Embedded circuit.
  • 
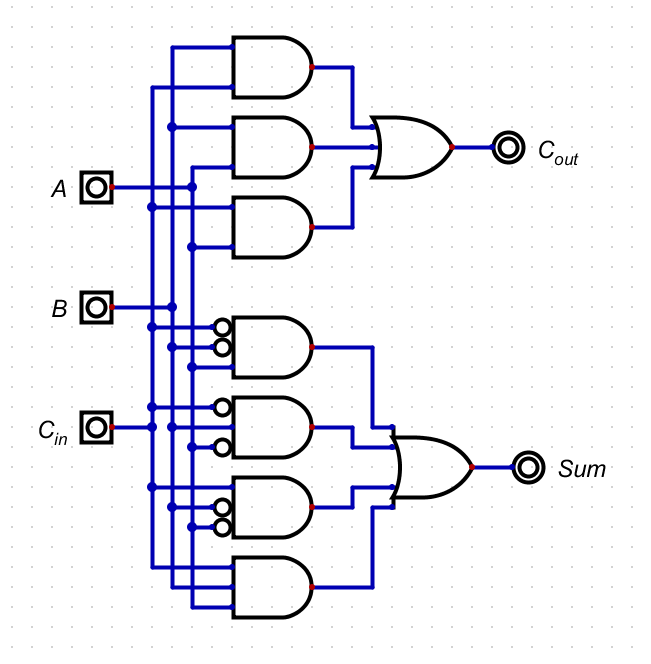
• We can then add this to our 1 bit ALU
  • 
• Here is a four bit version of an ALU (at least at this midpoint)
• 
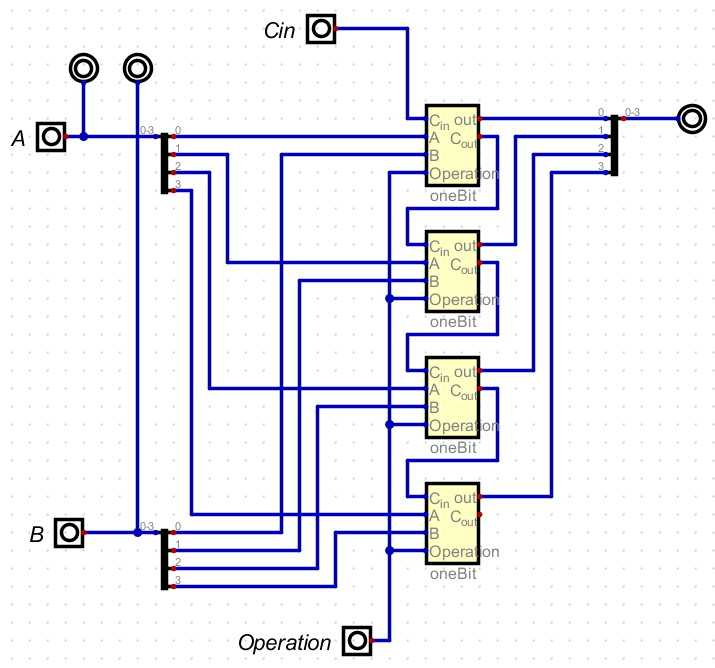
• The next step is to support subtraction.
  • This would be a-b
  • This is quite easy as all we need to do is invert b and add 1
  • We can use the carry in to add 1.
  • And modify the one bit alu
    • Add a control line for binvert
    • Use this to drive a mux to select between $b$ and $\overline{b}$.
    • 
• They state that we need a nor for mips.
  • $\overline{a+b} = \overline{a} \overline{b}$
  • So we can add an a invert, and an a invert line to accomplish this.
• They also add a less line.
  • This is for slt
    • An R type instruction
    • R[rd] = 1 if (R[rs] < R[[rt]]) otherwise 0
  • To do this, we are going to compute a-b
    • If it is a negative number, we will set the output to be 1
    • If it is a positive or 0 number, we will not.
    • So the less line will allow us to carry the "sign" bit from the last 1-bit ALU back to the first 1-bit ALU.
    • And this will be output 3 from the control

      Control Bits	Ainvert	Binvert	Operation
      00	0	0	and
      00	1	1	nor
      01	0	0	or
      10	0	0	a+b
      10	0	1	a-b
      11	0	1	slt

  • The last bit is for beq
    • If the two registers are equal, increment the pc by the immediate.
    • This can be done with a subtraction.
    • If all bits are 0, the numbers are the same.
    • So we will have the ALU do a-b, and an or of all of the resulting bits.